42: WorldToScreen
概要
EntityListの情報を元に作れる代表的なチートは Aimbot と ESP だと思います。 ESPチートとは、敵の場所や体力等を検出し、画面上で敵を囲ったり、その横に体力バーを表示したりするチートです。 しかし、2Dの画面上でワールドの3D座標で管理されている敵を囲う場合、ワールド座標から画面上の座標に変換する処理をしないといけません。 今回は、ワールド座標から画面上の座標に変換するWorldToScreenの仕組みを理解する事を目標にやっていきます。コンピューターグラフィックスでの4座標系と3変換
まず、一般的に3Dゲームのような所謂コンピューターグラフィックスには、 以下 4つの座標系 と 3つの変換 があります。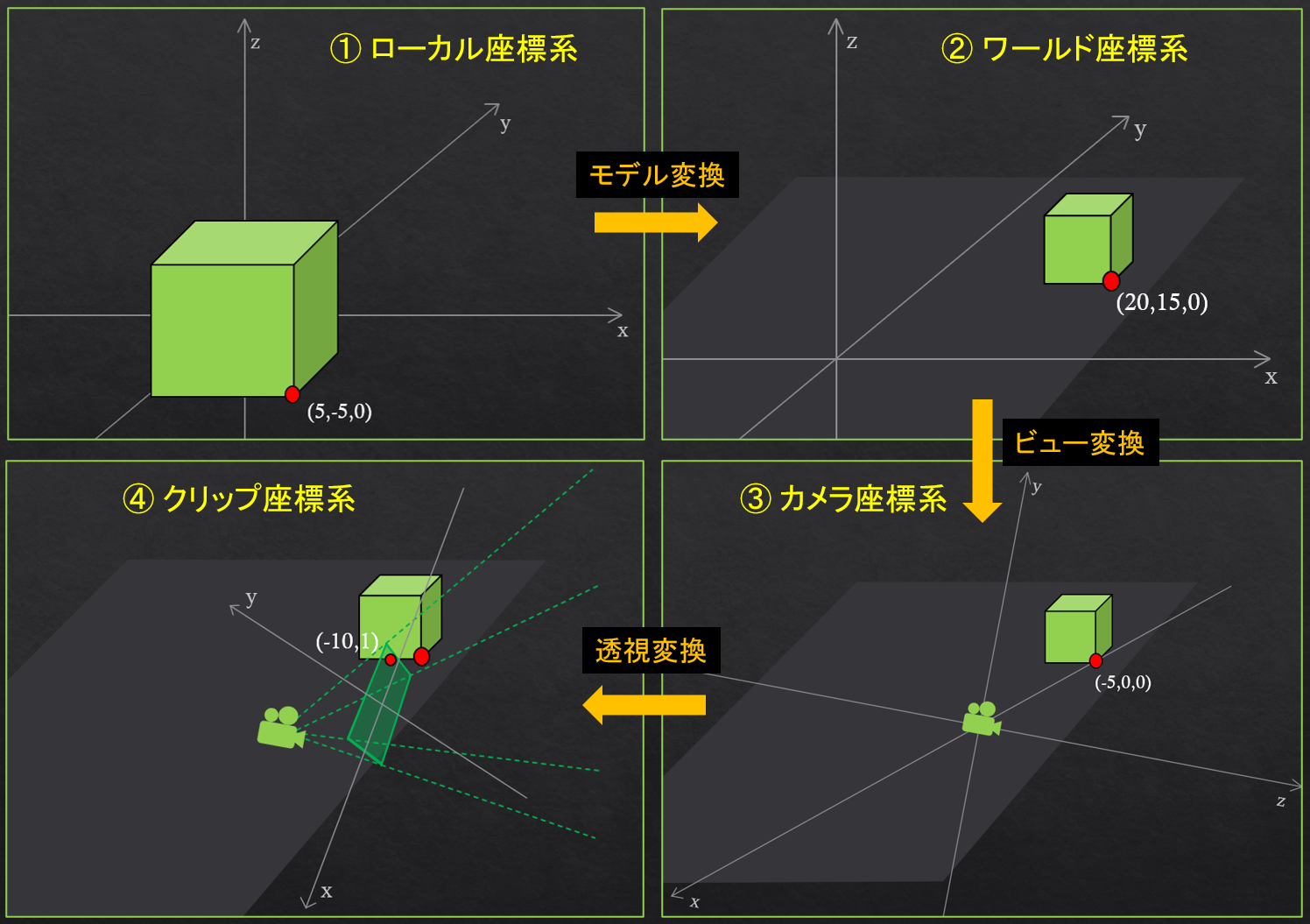
※ 座標の値は適当です。※ クリップ座標系からさらに色々変換とかもありますが、省略します。
4つの座標系の説明は以下です。
- ローカル座標系（モデル座標系）: 例えばプレイヤーの足を原点とした場合、足から見た頭の座標みたいな相対的な座標
- ワールド座標系: 今まで自分達が求めてきた座標で、ワールドのどこかを原点とし、そこからの敵の座標的な奴
- カメラ座標系（ビュー座標系）: カメラ(多くの場合プレイヤー)を原点とし、カメラから正面の方向をZ軸とした座標
- クリップ座標系: カメラの前の仮想的な平面内での座標（これをゲーム画面の横幅や高さに調整すればゲームウィンドウ上での座標になる）
一方、ある座標系からある座標系へ変換する事ができ、それぞれの変換に上図のように名前がついています。
この3つの変換の内、WorldToScreenはワールド座標を変換する物なので、ローカル座標系とモデル変換は忘れて大丈夫です。 また、透視変換はあくまでカメラの前の "仮想的な平面" 内での座標なので、この仮想的な平面を実際にゲームウィンドウの横幅/高さに調整する必要があります。
つまり、WorldToScreenはビュー変換と透視変換を主なった後、ゲームウィンドウの横幅/高さに合うように調整する処理となっています。
同次座標（斉次座標）
上述した3変換は具体的には、行列の掛け算で実装されています。 しかし、この仕組みを理解する前に同次座標という物を理解する必要があります。同次座標は、普通の座標に次元を一つ増やして表現する方法で、以下のように
(x,y,z,w) という同次座標があったら、
これは普通の座標の (x/w, y/w, z/w) と同じ意味となるというそれだけの座標です。| 同次座標 | 普通の座標 |
|---|---|
| (x, y, z, w) | (x/w, y/w, z/w) |
| (5, 10, 15, 5) | (1, 2, 3) |
何でわざわざこんな座標があるのかというと、この座標を使って行列を構成して演算する事で、 行列の掛け算でオブジェクトのあらゆる操作(移動/回転/スケーリング)が表せるからです。
ただ実は、回転とスケーリングは同次座標を使わなくても計算できます。
例えば回転に関しては、以下のように回転行列を回転させたいオブジェクトの各点に掛け算する事により実現できます。
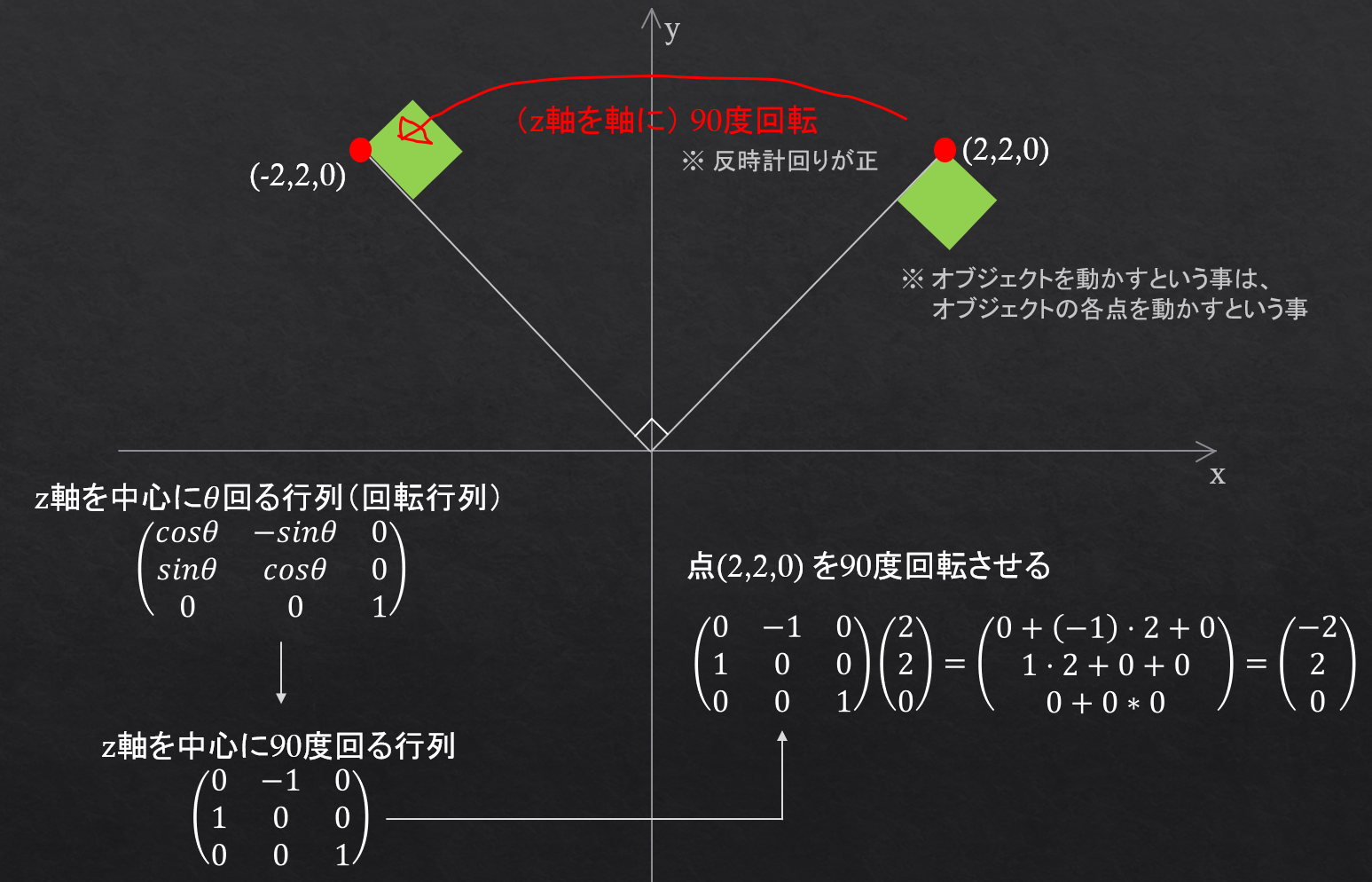また、スケーリングに関しては、以下のようにできます。
\[
\begin{bmatrix}S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & S_z\end{bmatrix}
\begin{bmatrix}x \\ y \\ z\end{bmatrix}
=
\begin{bmatrix}S_x x \\ S_y y \\ S_z z\end{bmatrix}
\]
※ (x,y,z)はワールド座標なので、スケーリングはワールドの原点を基準にスケールするので注意しかし、平行移動に関しては掛け算ではなく足し算です。 平行移動とはつまり、
(x,y,z) が (x+Nx, y+Ny, z+Nz) みたいな座標に移動するような挙動です。
これを行列の "掛け算" で表したい場合に、同次座標が意味を成してきて、以下のようにすればよくなります。
\[
\begin{bmatrix}1 & 0 & 0 & N_x \\ 0 & 1 & 0 & N_y \\ 0 & 0 & 1 & N_z \\ 0 & 0 & 0 & 1\end{bmatrix}
\begin{bmatrix}x \\ y \\ z \\ 1\end{bmatrix}
=
\begin{bmatrix}x+N_x \\ y+N_y \\ z+N_z \\ 1\end{bmatrix}
\Longrightarrow
\begin{bmatrix}x+N_x \\ y+N_y \\ z+N_z\end{bmatrix}
\]
もちろんですが、同次座標を用いても回転とスケーリングはできます。よって、同次座標を使うと移動/回転/スケーリングが行列の掛け算で表されるようになります。
モデル変換/ビュー変換/透視変換
ここまでの内容で、3Dグラフィックスには4座標系と3変換があり、変換とはつまり行列の掛け算の事で、 行列の掛け算でオブジェクトの移動/回転/スケーリングが表せるように同次座標というのを理解しました。ここで、何故そもそも掛け算で表す必要があるかと言うと、掛け算は以下のように行列を合成できて便利だからです。 \[ v' = PVM \cdot v \] ※ v'やvはベクトル、P,V,Mは行列です
これは、最初にベクトルvを行列Mにより何らか(移動/回転/スケーリング)の変換を行った後、行列Vをその結果にかけてまた変換、 最後にその結果に行列Pをかけて変換された座標がv'になっているという式です。
しかしこれは、先に 行列PとVとMの行列の積を求めて置き、それをvに掛けても同じ結果になります。 つまり、行列P,V,Mを合成した行列をvに掛けているという意味になります。
ここで実は、行列PとかVとかMは、先程の以下の変換になります。
- モデル変換 (Model Transformation)： 行列Mを掛ける
- ビュー変換 (View Transformation)： 行列Vを掛ける
- 透視変換 (Projection Trasformation)： 行列Pを掛ける
WorldToScreenでは、行列PVをワールド座標に掛ける事により、クリップ座標を得る処理という事になります。
ビュー変換の仕組み
WorldToScreenの処理を理解するには、ビュー変換と透視変換を理解すれば良い事になります。ビュー変換の仕組みからまず説明していきます。
ビュー変換は少しややこしいので、まずは簡単のため二次元(xy平面)で考え、同次座標も使わず、 カメラがワールド座標の原点と同じ位置にある状況で考えてみます。また、大体はカメラの正面の方向の軸はz軸ですが、それも一旦無視します。
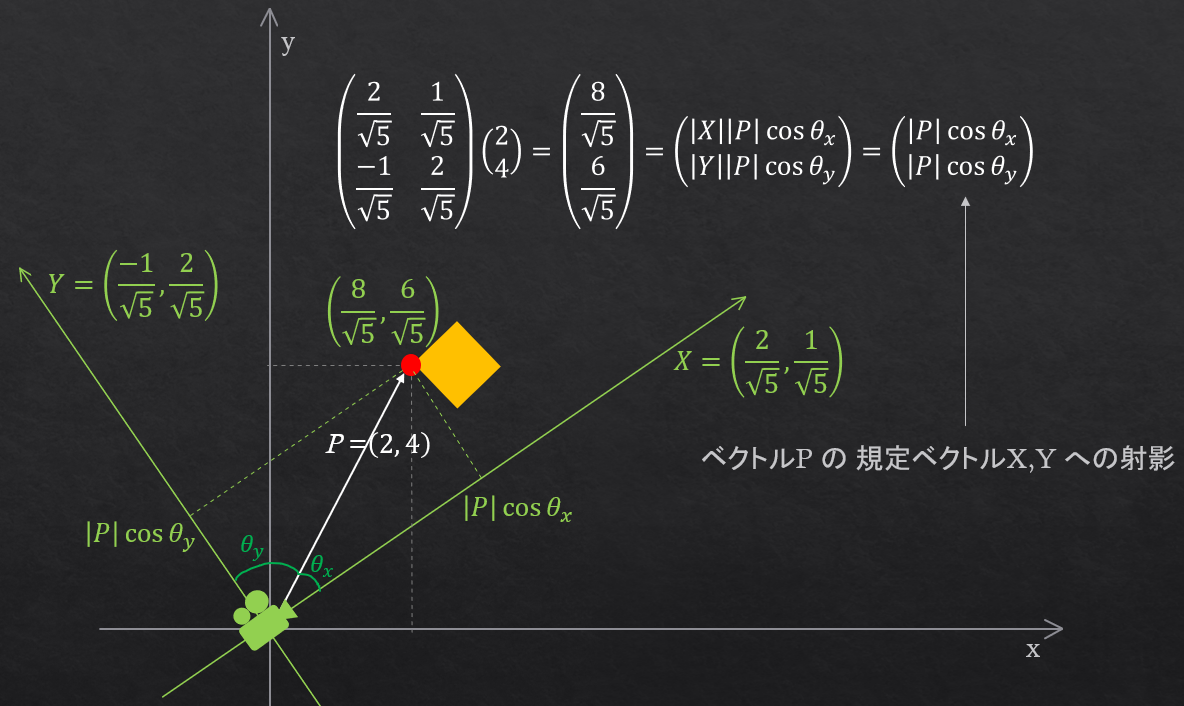灰色のXY軸がワールド座標軸で、赤色の点の座標がベクトルP (2,4) で表されていたとします。
このPの座標を、黄緑色のカメラの座標軸上での座標に変換するのがビュー変換です。結論から言うと、この場合ビュー変換は、ベクトルPにカメラの座標系の基底ベクトルを並べた行列(これがビュー行列)を掛ける事により、実現できます。
※ 基底ベクトルとは、座標軸の各軸のベクトルの事で、長さを1にした物です。
なぜこれで変換できるかというと、基底ベクトルを上図のように並べた行列をベクトルPと掛けるという事は、 各基底ベクトルとベクトルPとの内積を取っているという事になります。内積は、各要素の積の和以外にも
|X||P|cos(θx)
のようにも表す事ができる訳ですが、基底ベクトルの大きさは1なので、|P|cos(θx)
と等しくなり、θx はPとXとの成す角なので、|P|cos(θx)
は図のようにカメラのx軸上での長さになります。yの方も同様です。これで、カメラのx軸上でこの長さ、y軸上でこの長さという値が求まるので、カメラの座標軸上での座標が求まったと言う事になります。
では、今度はカメラをワールド座標
(2,2) に動かし、同次座標を導入してみます。(同次座標にするので要素3つになってますが、z座標は追加されていないので注意)
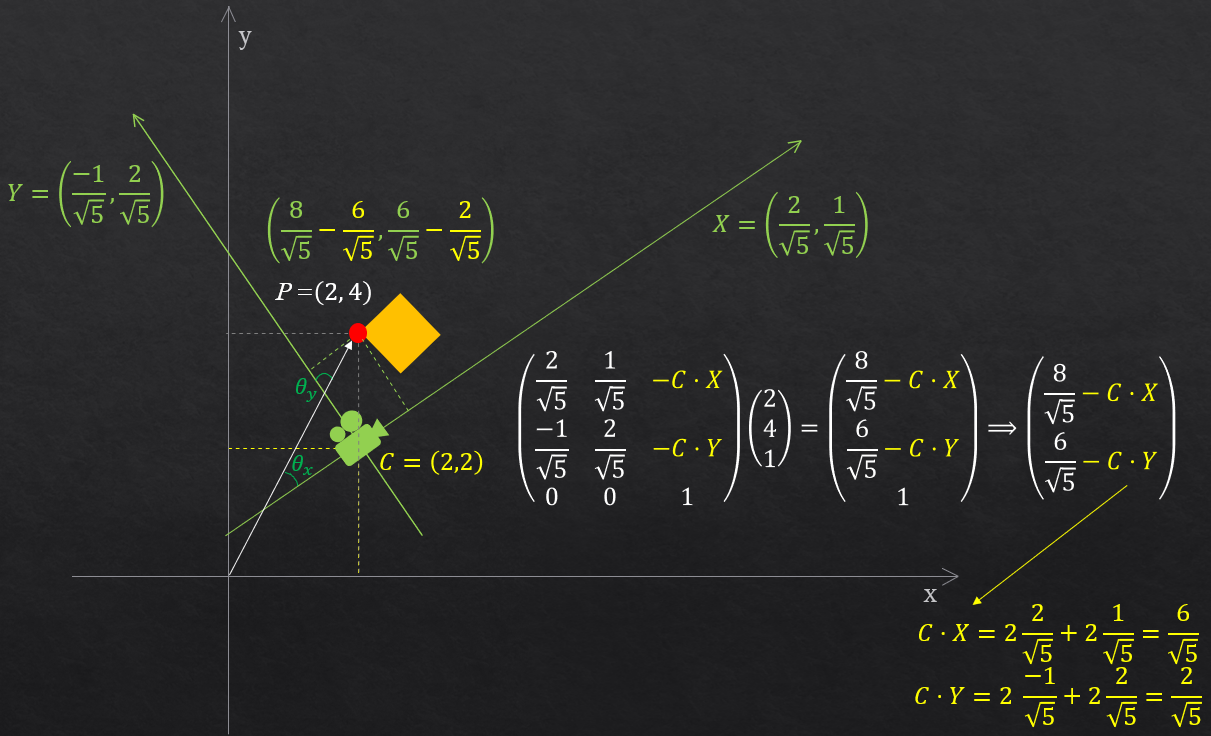先程の図と比べてみるとわかりますが、基底ベクトルが変わるわけではない(カメラの向きが変わるわけでは無い)
ので、ビュー行列の一列目と二列目の要素は先程と同じ値です。しかし、カメラの座標系が全体的に平行移動しているため、
相対的にワールドは逆向きに動くので、その平行移動の処理分をビュー行列の黄色い部分に追加しなければなりません。カメラがワールドの原点から
(2,2) に動いたからといって、(-2,-2) ただ移動すればいいというわけではありません。
これは例えばカメラを (2,4) に動かした場合、赤い点はカメラの座標軸の原点に来るはずですが、(-2,-4)
動かしても0にならない事からわかると思います。実際は、上図のようにカメラの座標と基底ベクトルとの内積分を引かないと行けません。
なぜそうするかというと、これも先程と同様に、例えばx軸の場合は、C・X = |C||X|cosθx = |C|cosθx
という意味になるので、カメラの座標軸上でどれくらいの距離なのかというのに換算してから、それを引いてるという意味になります。よって、ビュー行列を構成するのに必要な要素は、以下の二つです。
- カメラの基底ベクトル(カメラの向き)
- カメラのワールド座標
このビュー行列をあらゆるワールド座標に掛ける事で、カメラ座標に変換できます。
透視変換
透視変換の方はただのスケーリングです。ただ、その前に少しカメラ関連の用語を説明します。
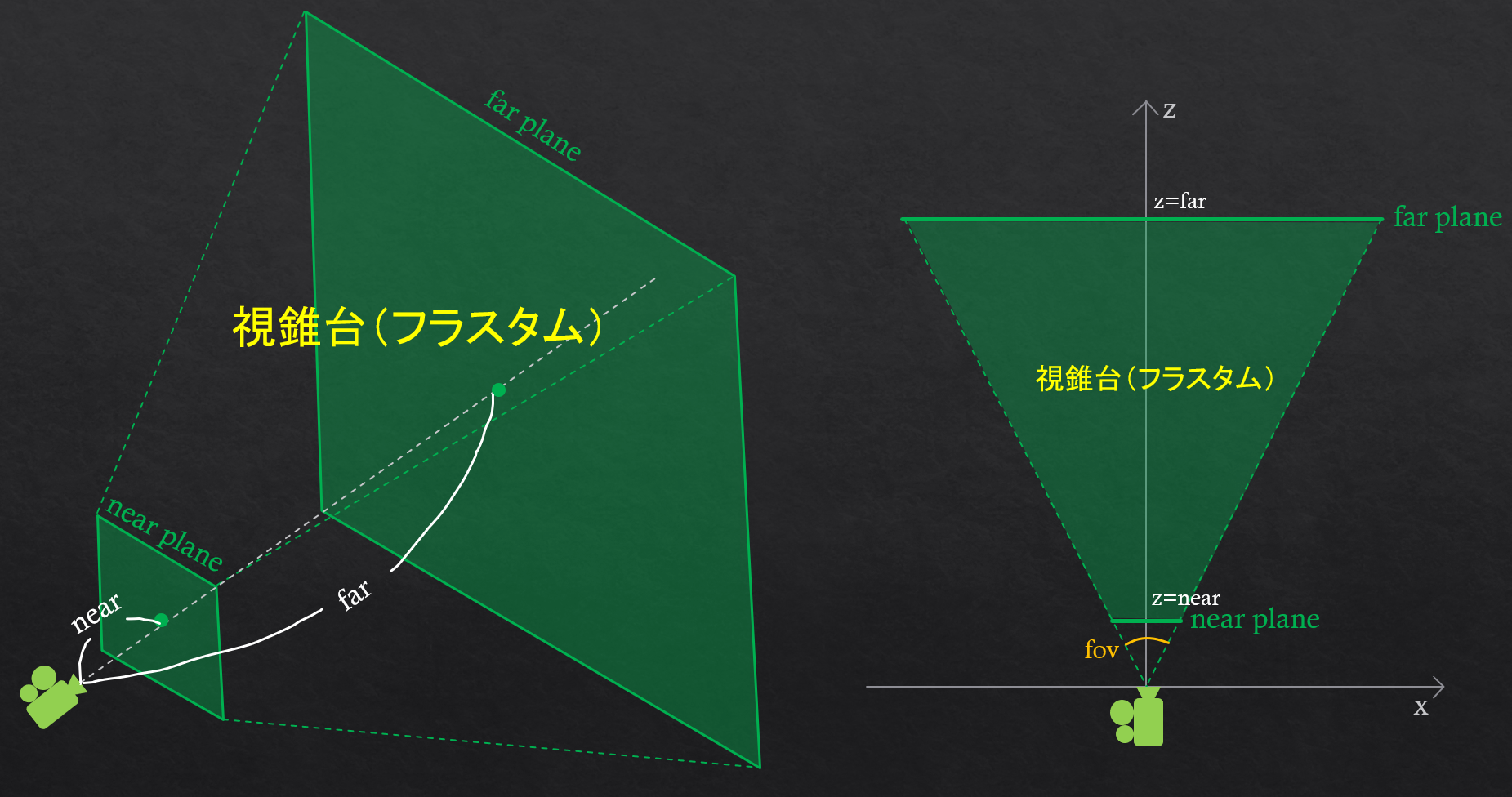まず、カメラが描画する領域の事を 視錐台 (フラスタム) と言います。
この視錐台の中にあるオブジェクトしか描画しない事になっており、例えば自分の真横にいる敵は視野に入らないので描画せず、
遠すぎる敵も描画しないみたいになってます。また、現実とはちょっと違う点が、近すぎる物も描画していない点です。上図で言う、
near plane とカメラとの間に、長さnear分の隙間がありますが、そこにある物も描画されません。視野の幅は、fov(画角) により定義されています。画角が大きい程視野が広がるといった感じです。 現実だとfovは180度ぐらいある気がしますが、ゲームだと90度あたりがよくある値らしいです。
透視変換は、下図のように視錐台内にあるオブジェクトを near plane に投影します。
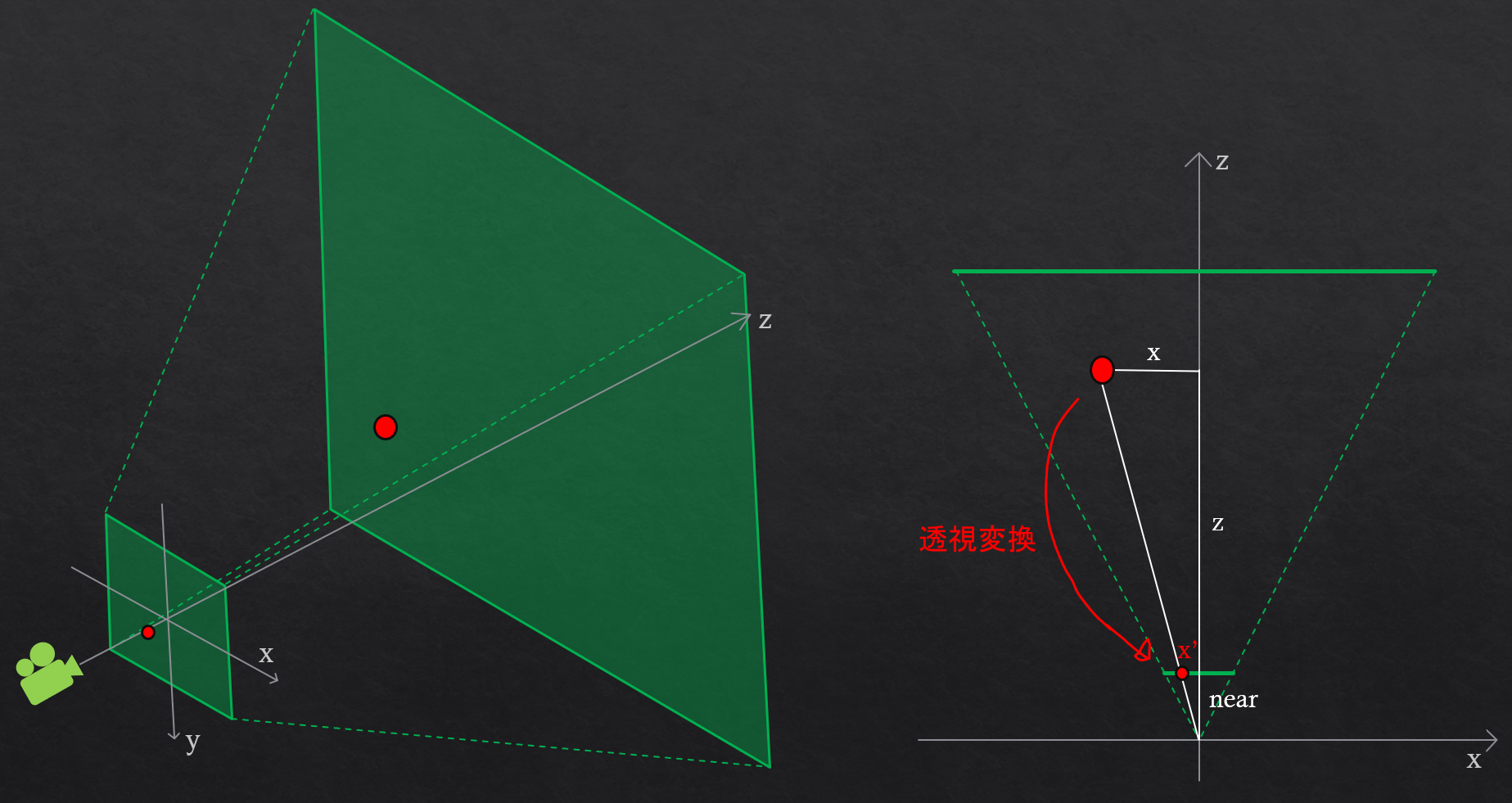求めたいのは、near plane上でのx座標(とy座標)なので、上図の右の図でいう x'
を求めれば良いことになります。これは相似の関係で求める事ができます。
\[z:x = near:x'\]
\[x'=\frac{near}{z}x\]
y座標も同じように求めればよく、これで実は透視変換は終了です。これを行列の掛け算で表すとしたら、以下のようになります (zはどうせ無視するので0にしてます)。 \[ \begin{bmatrix}near & 0 & 0 & 0 \\ 0 & near & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix} \begin{bmatrix}x_{cam} \\ y_{cam} \\ z_{cam} \\ 1\end{bmatrix} = \begin{bmatrix}near \cdot x_{cam} \\ near \cdot y_{cam} \\ 0 \\ z_{cam}\end{bmatrix} = \begin{bmatrix}\frac{near}{z_{cam}} \cdot x_{cam} \\ \frac{near}{z_{cam}} \cdot y_{cam} \\ 0 \\ 1\end{bmatrix} \Longrightarrow \begin{bmatrix}\frac{near}{z_{cam}} \cdot x_{cam} \\ \frac{near}{z_{cam}} \cdot y_{cam} \\ 0\end{bmatrix} \] つまり、行列Pは以下になります。 \[ P=\begin{bmatrix}near & 0 & 0 & 0 \\ 0 & near & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix} \] ※ ワールド座標系では上がy軸正、クリップ座標系では下がy軸正となっていて、yをマイナスする場合もあります
ちなみに他のサイトで行列Pを見ると、これよりもっと複雑な行列になってると思います。
これは、実は透視変換の本来の意味は、自分が説明した物とは少し違うからです。
本来は、透視変換はNDCという辺の長さ1の立方体内での座標に一度変換するものです(たぶん)。 また、今回自分は勝手に、視錐台が左右対称である、near planeの横幅と縦幅の比率が実際のゲームウィンドウの横幅と縦幅の比率と同じである と仮定もしています。その他にも、自分が見落としてる点もあるかもしれません。
しかし、大体のゲームでは視錐台は左右対称（右の方が長いとか無さそう）ですし、 チートする側としては、単に ワールド座標からスクリーン座標(ゲームウィンドウ画面上での座標)に変換する(その過程はどうでもいい) 事だけが目的なので、既存の変換手順にきっちり従わなくても、チートに必要無い所は省くスタイルで進めて行こうと思います。
スクリーン上での座標に変換
ビュー変換と透視変換というメインの変換が終りましたが、最後の微調整として、near plane をウィンドウサイズの大きさにスケールする という作業があるのでそれをやります。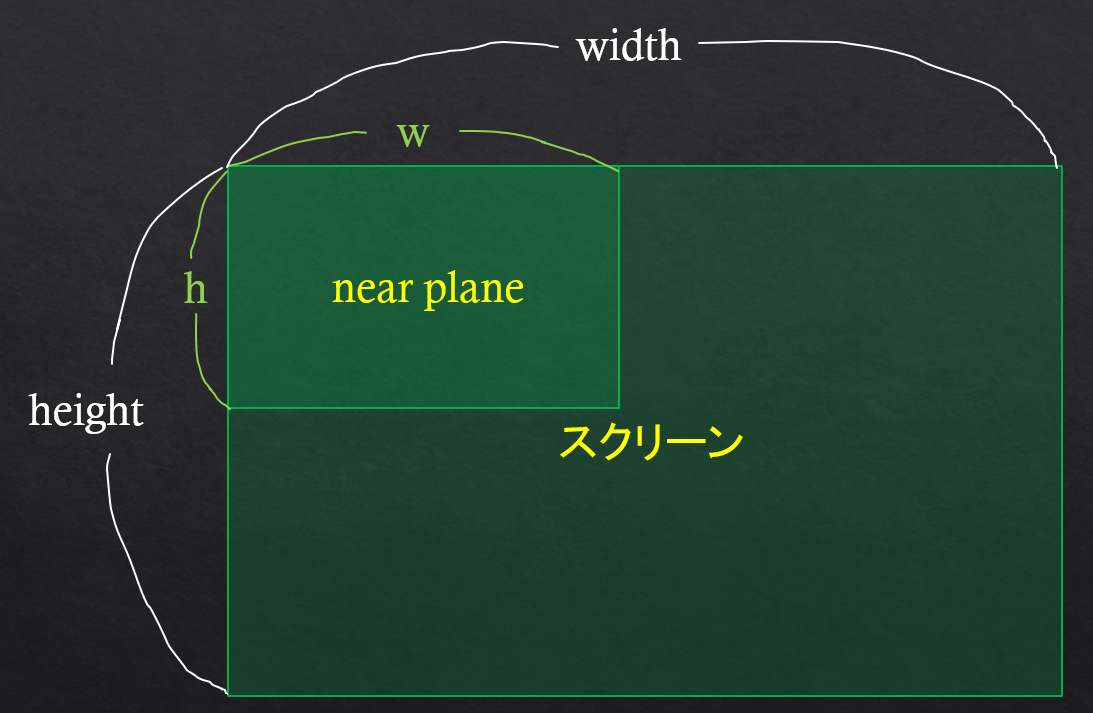
これも相似の関係で、x座標は width/w倍、y座標は height/h倍
すればいいだけです。※ near planeの横幅と高さの比が実際のスクリーンの比(正確にはゲームウィンドウの横幅と高さの比)と同じという仮定
wとhの求め方に関しては、まずwは以下のように求められます。
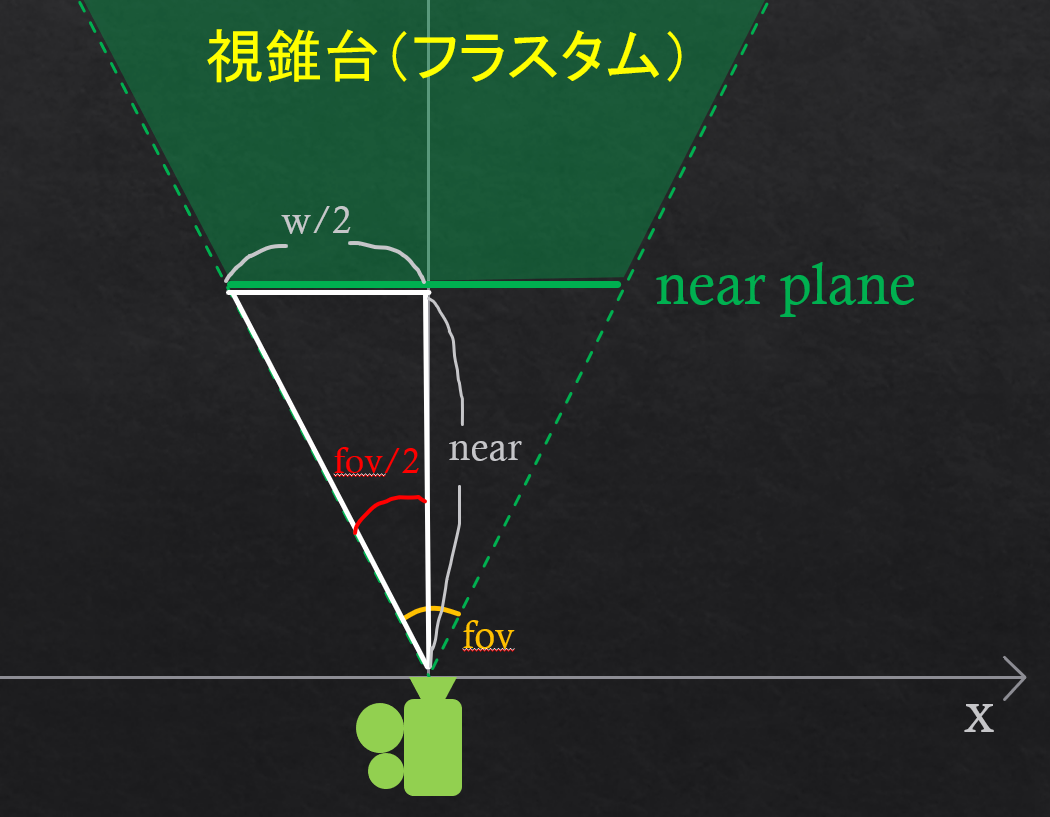\[tan(fov/2) = \frac{w/2}{near}\]
\[w = 2 \cdot near \cdot tan(fov/2)\]
hに関しては、二個上の図の相似の関係を使って、以下のように求められます。
\[h = \frac{height}{width}w\]
なので、最終的には以下のようにすれば、クリップ座標からゲームウィンドウ上での座標に変換できます。
\[ x_{screen} = \frac{width}{w}x_{clip} = \frac{width}{2 \cdot near \cdot tan(fov/2)} x_{clip} \]
\[ y_{screen} = \frac{height}{h}y_{clip} = \frac{width}{w}y_{clip} = \frac{width}{2 \cdot near \cdot tan(fov/2)} y_{clip} \]
これで一見終わりに見えるのですが、実はクリップ座標とスクリーン座標では、以下のように原点が違います。
上述の計算までだと、スクリーンでも原点が真ん中にある場合の座標になっているので、以下のように横幅と高さの半分の値を足す必要があります。
\[ x_{screen} = \frac{width}{2 \cdot near \cdot tan(fov/2)} x_{clip} + \frac{width}{2} \]
\[ y_{screen} = \frac{width}{2 \cdot near \cdot tan(fov/2)} y_{clip} + \frac{height}{2} \]
WorldToScreen関数まとめ
まとめると、WorldToScreenはビュー変換と透視変換を行い、最後ゲームウィンドウの横幅/高さに調整する処理であり、 数式で表すと以下になります。 \[ \begin{bmatrix} x_{clip} \\ y_{clip} \\ 0 \\ 1\end{bmatrix} = PV \begin{bmatrix} x_{world} \\ y_{world} \\ z_{world} \\ 1 \end{bmatrix} = \begin{bmatrix}near & 0 & 0 & 0 \\ 0 & near & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix} \begin{bmatrix}X_x & X_y & X_z & -P \cdot X \\ Y_x & Y_y & Y_z & -P \cdot Y \\ Z_x & Z_y & Z_z & -P \cdot Z \\ 0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix} x_{world} \\ y_{world} \\ z_{world} \\ 1 \end{bmatrix} \] \[ x_{screen} = \frac{width}{2 \cdot near \cdot tan(fov/2)} x_{clip} + \frac{width}{2} \] \[ y_{screen} = \frac{width}{2 \cdot near \cdot tan(fov/2)} y_{clip} + \frac{height}{2} \] これをプログラムにすれば、WorldToScreenの出来上がりです。しかし、これ実はよくみると
nearが要らない事がわかります。クリップ座標を、カメラの座標系での座標で表すと、 \[ \begin{bmatrix} x_{clip} \\ y_{clip} \\ 0 \\ 1\end{bmatrix} = \begin{bmatrix}near & 0 & 0 & 0 \\ 0 & near & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix} \begin{bmatrix}X_x & X_y & X_z & -P \cdot X \\ Y_x & Y_y & Y_z & -P \cdot Y \\ Z_x & Z_y & Z_z & -P \cdot Z \\ 0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix} x_{world} \\ y_{world} \\ z_{world} \\ 1 \end{bmatrix} = \begin{bmatrix}near & 0 & 0 & 0 \\ 0 & near & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix} \begin{bmatrix} x_{cam} \\ y_{cam} \\ z_{cam} \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{near}{z_{cam}} \cdot x_{cam} \\ \frac{near}{z_{cam}} \cdot y_{cam} \\ 0 \\ 1 \end{bmatrix} \] の数式により、以下になります。 \[ x_{clip} = \frac{near}{z_{cam}} \cdot x_{cam} \] \[ y_{clip} = \frac{near}{z_{cam}} \cdot y_{cam} \] これを、スクリーン座標への変換の式に当てはめると、以下のようになり、
near が消えることがわかります。
\[ x_{screen} = \frac{width}{2 \cdot near \cdot tan(fov/2)} x_{clip} + \frac{width}{2} \]
\[= \frac{width}{2 \cdot near \cdot tan(fov/2)} \frac{near}{z_{cam}} \cdot x_{cam} + \frac{width}{2} \]
\[= \frac{width}{2 \cdot tan(fov/2) \cdot z_{cam}} \cdot x_{cam} + \frac{width}{2}\]
※ yも同様これはつまるところ、透視変換とスクリーン座標への変換の処理を合わせると
near が消えるという事なので、
透視変換も行列でわざわざ表さずにスクリーン座標への変換の処理と組み合わせてしまい、最終的に以下のようにすれば、
より良いWorldToScreenになります。よって、最終的なWorldToScreenの処理は以下になります。 \[ \begin{bmatrix} x_{cam} \\ y_{cam} \\ z_{cam} \\ 1\end{bmatrix} = V \begin{bmatrix} x_{world} \\ y_{world} \\ z_{world} \\ 1 \end{bmatrix} = \begin{bmatrix}X_x & X_y & X_z & -P \cdot X \\ Y_x & Y_y & Y_z & -P \cdot Y \\ Z_x & Z_y & Z_z & -P \cdot Z \\ 0 & 0 & 0 & 1\end{bmatrix} \begin{bmatrix} x_{world} \\ y_{world} \\ z_{world} \\ 1 \end{bmatrix} \] \[ x_{screen} = \frac{width}{2 \cdot tan(fov/2) \cdot z_{cam}} \cdot x_{cam} + \frac{width}{2} \] \[ y_{screen} = \frac{width}{2 \cdot tan(fov/2) \cdot z_{cam}} \cdot y_{cam} + \frac{height}{2} \] ※ 尚、X,Y,Z はカメラの基底ベクトル(X=Xx,Xy,Xz)、Pは変換対象のワールド座標 \[P=(x_{world}, y_{world}, z_{world})\]