17: プレイヤーの向き(クォータニオン)の取得
概要
プレイヤーを "前" に動かしたり、エイムボットを作ったりする場合、座標だけでなく向きの情報も必要となってくる。3Dゲームでは、向きあるいは回転は、しばしばクォータニオンという方法で表現されるが、 座標みたいにジャンプすればy座標の部分が上がるといったように直観的にプレイヤーの動きと数字の変化が結びつく物ではないので、意外と厄介な物である。
今回は、クォータニオンとは何かとクォータニオンからプレイヤーの前後左右上下のベクトルを算出する方法について知り、プレイヤーのクォータニオンを特定する事を目標にやっていきます。
チート対象のゲームは、x86でチートの練習用に作られた、Pwn Adventure 3を使います。
クォータニオンとは
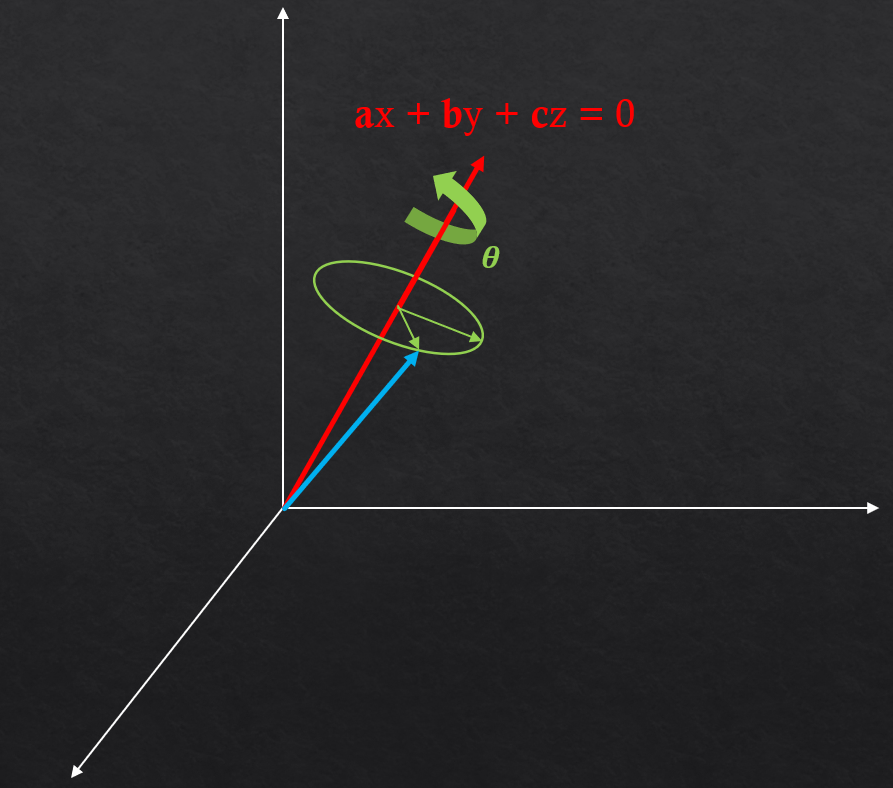 上図のように、回転軸
上図のように、回転軸 ax+by+cz=0 の周りを、角度 θ 回った時の向き(青い線)をクォータニオンで表した物が以下。
(x, y, z, w) = (a sin(θ/2), b sin(θ/2), c sin(θ/2), cos(θ/2))θ はラジアンである※ 普通の角度 => ラジアン をするには
π/180 をかければよい※ 回転軸のベクトル
(a,b,c) は 単位ベクトル(長さが1) である必要があるクォータニオンから前後左右上下のベクトルを取得
前
x = 2 * (x*z + w*y)
y = 2 * (y*z - w*x)
z = 1 - 2 * (x*x + y*y)上
x = 2 * (x*y - w*z)
y = 1 - 2 * (x*x + z*z)
z = 2 * (y*z + w*x)左
x = 1 - 2 * (y*y + z*z)
y = 2 * (x*y + w*z)
z = 2 * (x*z - w*y)(-x,-y,-z)にすればよい。※ ココを丸パクリした。
実際はプレイヤーではなくカメラの向きを取得する
ここで少し整理しておきたいのは、プレイヤーの座標と向きがあるのとは別に、カメラの座標と向きもあるという点である。今回、「プレイヤーの向き」を取得すると言ったが、実際は「第三者視点の時のカメラの向き」を取得しようと思う。
理由は単純に、プレイヤーの向きの情報が自分には特定できなかったのと、このゲームではカメラとプレイヤーの向きが常に連動していて同じなので、支障は無いからである。
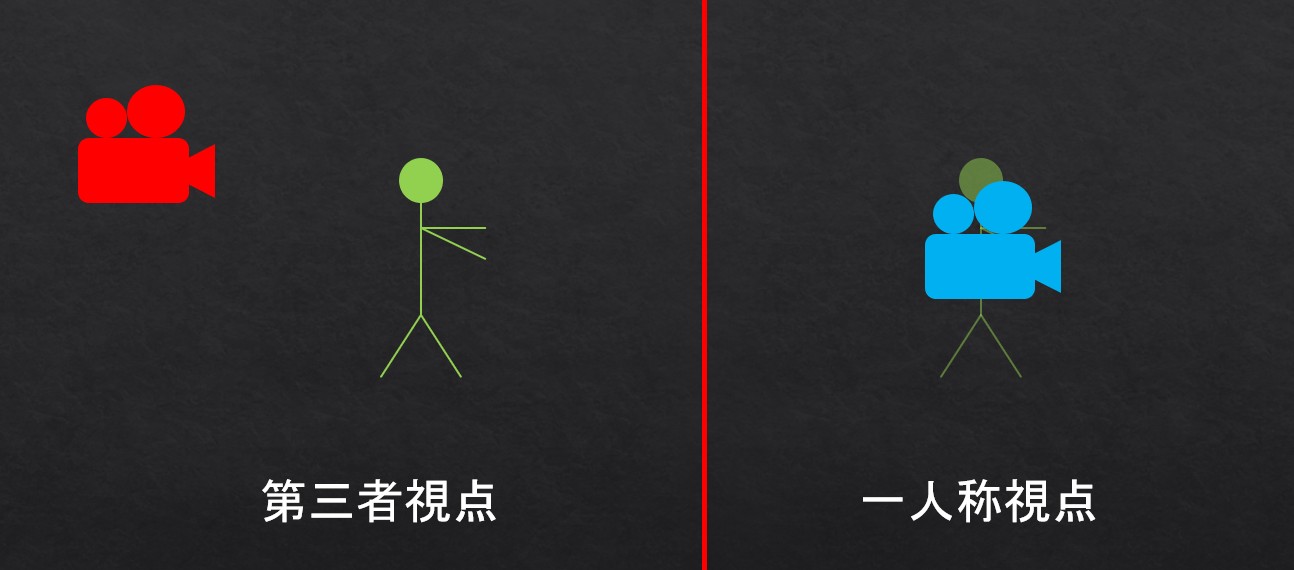 PwnAdventure3では、
PwnAdventure3では、pキーを押せば、一人称視点と第三者視点を切り替える事ができる。ここで注意すべきなのは、
このゲームでは、どっちの視点かで使ってるカメラのオブジェクトが違うという点である (後述する方法で実際に二パターンでアドレスを特定してみるとわかる)。
つまり、一人称視点でカメラの座標や向きがわかったとしても、第三者視点の方の座標や向きの情報は別のアドレスにあるという事である。カメラの向きの取得方法の概要
"向き" は直観的ではないクォータニオンで表現されているため、座標のようにジャンプしてCheatEngineで "今増えた値" のようにフィルターを掛けて特定する事ができない。 しかし、ゲームを作る側の視点に立つと、座標と向きという情報は同じカメラオブジェクトの動きに関する情報という点で似ているため、近くにある可能性が高い。よって、まずカメラの座標を特定し、その周辺のメモリを覗き、クォータニオンっぽいアドレスを特定する。
では、カメラの座標はどうやって特定するのかと言う点だが、第三者視点のゲームでは、通常プレイヤーとカメラのオブジェクトが上図のようにグループ化されて動いている。
つまり、プレイヤーがジャンプすれば、カメラのy座標も上がるはずである。
よって、カメラの座標はCheatEngineでプレイヤーの座標と同じように特定できる。
カメラの向きの取得
カメラの座標をプレイヤーの座標を取得するのと同じように特定した後、その周辺のメモリを見てみる。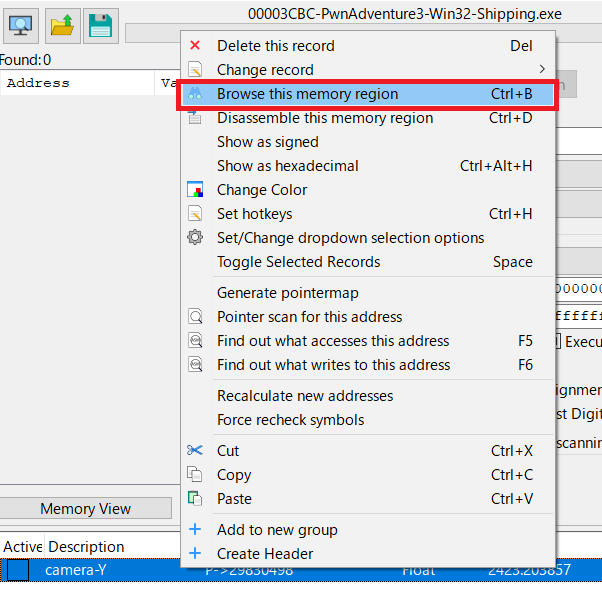 上記の
上記のBrowse this memory regionで見れるのは機械語の羅列なので、このまま見ても意味不明だが、CheatEngineは優秀な事に変化があった場所を赤くハイライトしてくれる。例えば、現在カメラのy座標のアドレスを見ているので、プレイヤーの向きを動かさずにプレイヤーを動かしてみて、そのアドレス周辺を見てみると、以下のように赤くなっている事がわかる。
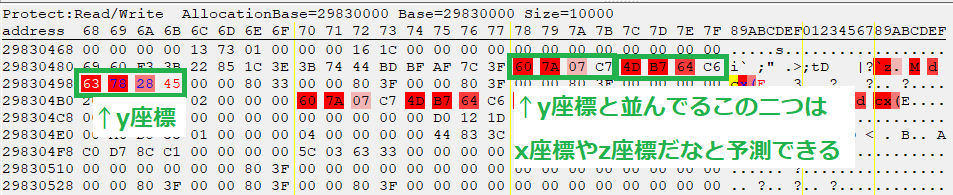 ちなみに、座標はおそらく
ちなみに、座標はおそらくfloat型で、float型は4Byteなので、上記のように4つで一括りに選択している。
では今度はプレイヤーを移動させずに、視点だけ移動させて変化を見てみる。
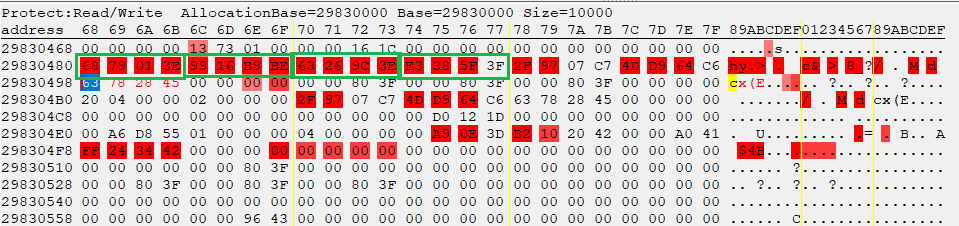 上記のように、座標の近くで、おそらく
上記のように、座標の近くで、おそらくfloat型(4Byte)で4つ連続で並んで動いているのがクォータニオンである可能性が高い。実際に上記のアドレスを追加してみて、値をいじってゲーム上の変化を見れば向きが変わるはずであり、これがクォータニオンであることがわかる。 上図で青くなってるところがカメラのy座標のアドレスなので、カメラのy座標から
29830498-29830480=0x18 引いたアドレスがクォータニオンのアドレスである事がわかる。
クォータニオン(や座標)の注意点
これでクォータニオンのアドレスは取得できましたが、注意すべき点は、上記の4つのどれがx だとか、どれが w かというのは実際に試さないと分からないという点です。つまり、
x, y, z, w の順だったり、y, z, x, w の順だったりと、愚直に言えば24通りあり、どの順が正解なのかは、上記で紹介した前後左右上下のベクトルの公式に当てはめてみて、
実際にそれで前に動くか等を試してみるまでわからないという事です。より厄介な事に、ゲーム上でy座標は確実にわかっても、x座標とz座標に関してはわからないので、適当にどっちかを決めないといけません。 また、そもそもx座標やz座標がどっち側を正としているかもわかりません。
よって、クォータニオンで全24通りを試しても、前上左が全部公式通りにマッチしない事もあります (例えば左右前後は公式通りなのに、上下だけ反転していたりなど)。
なので、あまり上記の公式にこだわらず、例えばクォータニオンの並び順を
w, y, x, z としたときに、
上記の公式に当てはめてその方向に動かしてみると、左右前後はちゃんと動いて、上下だけ反転していた場合は、
yが逆向きになっているという事なので、以下のように公式を変えちゃって辻褄を合わせた方が良いです (全部の y= に *(-1) をつける)。
前
x = 2 * (x*z + w*y)
y = 2 * (y*z - w*x) * (-1)
z = 1 - 2 * (x*x + y*y)上
x = 2 * (x*y - w*z)
y = (1 - 2 * (x*x + z*z)) * (-1)
z = 2 * (y*z + w*x)左
x = 1 - 2 * (y*y + z*z)
y = 2 * (x*y + w*z) * (-1)
z = 2 * (x*z - w*y)w, y, x, z の並び順で、公式を上記のようにして適用しています。
